PERANAN CABRI GEOMETRI DALAM PEMBELAJARAN GEOMETRI SMP

Berikut adalah beberapa contoh eksplorasi Cabri Geomtry dalam pembelajaran geometri siswa SMP:

1.      Menggunakan Cabri Geometry Untuk Mengembangkan Logika Pembuktian

Salah satu aturan dalam pembelajaran geometri di kelas adalah bagaimana siswa mengungkapkan bukti dengan adanya fakta-fakta. Sebuah bukti akan diterima secara logis apabila sesuai dengan definisi,  aksioma dan teorema sebebelunya.
Menurut Mariotti (1997) Untuk membantu siswa memahami logika pengembangan bukti menggunakan ide-ide yang dimiliki olehh siswa diperlukan sebuah media yang dapat menggambarkan situasi dari sebuah teorema. Dibawah ini adalah contoh pebuktian dari sebuah teorema yang kemudian di konstruksi dengan menggunakan Cabri Geometry dan siswa kemudian menentukan nilai kebenaran darisebuah teorema tersebut.

No.	Pernyataan	Pembenaran (jastifikasi)	Konstruksi di Cabri dan terkait langkah-langkah dalam bukti
1	A, B dan C adalah titik-titik yang tidak segaris (non coliner)	Diberikan	Gambarkan titik-titik A, B dan C yang tidak dalam satu garis (1)
2	Garis yang melalui titik A dan B ada	Postulat garis	Gambarkan Garis yang melalui titik A dan B (2)
3	segmen AB ada	Definisi segmen garis	Gambarkan segmen AB (3)
4	Jika M adalah titik tengah segmen AB	Teorema titik tengah	Temukan titik tengah M pada segmen AB (4)
5	Garis yang melalui titik C dan M ada	Postulat garis	Gambarkan Garis yang melalui titik C dan M (5)
6	CM = r, r>0	Postulat jarak
7	Misalkan 0 dan r dari masing-masing titik C dan M	Postulat tempat kedudukan dan kuasa titik	Menggunakan busur, lingkaran dan pemindahan ukuran (perlu menemukan panjang CM langsung atau tidak langsung) (6)
8	Misalkan D terletak pada CM sehingga yang koordinat D adalah 2r.	Postulat kuasa titik	Gambar titik D pada CM (8)
9	0 < r < 2r	Sifat bilangan real	Pastikan bahwa M adalah titik tengah dari CD. (10, 12)
10	C-M-D	Teorem antara pertama
11	CM = r – 0 = r, DM = 2r – r = r.	Postulat kuasa titik
12	CM = DM.	Sifat Transitif
13	M adalah titik tengah segmen CM	Definisi titik tengah
14	Segmen AB dan CD membagi dua satu sama lain	Definisi pembagian

Langkah-langkah pembelajarannya:

  Contoh: Pada postulat pertama siswa diberikan tiga buah titik A, B, dan C.

Dari gambar terlihat bahwa titik A, B dan C tidak segaris. Kemudian Siswa dapat membuktikan bahwa garis yang melalui titik A dan B ada.

 

Dengan mengkonstriksi garis tersebut siswa telah membuktikan postulat dari sebuah garis yaitu : Dua buah titik hanya dapat ditarik sebuah garis lurus. Selain itu, siswa juga dapat membenarkan bahwa segmen AB itu ada yaitu erletak pada garis l dan seterusnya sesuai dengan apa yang ada di dalam tabel.

Kemudian, setelah sebmua siswa melakukan konstruksi yang sama di Cabri Geometry, siswa diminta  untuk membandingkan langkah-langkah konstruksi dengan pernyataan dan pembenaran bukti, yang memimpin mereka untuk menyertakan nomor langkah bukti (diberikan dalam kurung) setelah setiap kalimat dan yang membantu mereka memahami hubungan antara bukti dan konstruksi.

                                                

2.      Menggunakan Cabri untuk membantu siswa mengembangkan ide untuk bukti

Untuk mengembangkan ide siswa dalam pembuktian yaitu dengan menggunakan masalah terbuka. Interaksi siswa dengan Cabri Geometry terjadi diamana setiap informasi yang dibutuhkan oleh siswa sudah tersedia dalam gambar yang dikinstruksi dalam Cabri Geometry.

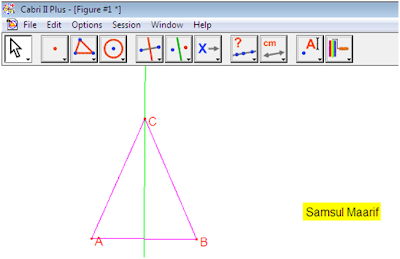
Contoh: Setelah siswa mempelajari segitiga sama kaki siswa dihadapkan pada masalah sebagai berikut: “Diketahui segitiga sama kaki ABC diman AC = BC. Titik P terletak pada sisi AB. Permasalahannya: dimana tepatnya letak titik P sehingga jarak P terhadap AC sama dengan jarak titik P ke  BC.

Tentunya terlebih dahulu di suruh untuk mengkonstruksi segitiga sama kaki. yaitu dengan cara membuat segmen AB dengan perintah tombol Segment => buat garis sumbu segmen AB dengan tombol Perpendicular Bisector => letakan titik C pada garis sumbu tersebut => buatlah segitiga ABC dengan tombol Triangle.

Letakan titik P pada sisi AB dengan tombol Point on Object => Buat garis tegak lurus AC melalui P dan garis tegak lurus AC melalui P dengan tombol Perpendiculer Line => Dengan tombol Distance and Lengt tentiukan jarak P ke AC dan P ke BC=> kemudian jumlahkan kedua jarak tersebut dengan tombol Calculate

Geser titik P kekanan dan kekiri biarlah siswa menyimpulkan sendiri. (Tentunya jawbanya adalah jumlah keduanya akan selalu sama).

Setelah siswa dapat menyimpulkan eksplorasi tersebuat biarlah mereka melakukan eksplorasi dengan pembuktin menggunakan aksioma atau postulat yang ada. Tentunya jawaban yang kita inginkan dari siswa adalah sebagi berikut:

Dari gambar cabri permasalah di atas buatlah garis sejajar dengan salah satu garis tinggi tersebut deng tombol Parralel Line.

 Dari gamabar diatas segitiga BPQ kongruen dengan segitiga BPE sehingga PE (jarak P ke BC) = BG. Dari konsep kesejajaran DP (jarak P ke AC) = FG, sehingga PE + DP = FG + BG = FB (Selalu sama dimanapun titik P berada).

 

3.      Menggunakan Cabri untuk membantu siswa memahami hubungan ketergantungan antara sifat

Pada kegiatan ini Ssiswa diminta mengeksplorasi masalah terbuka kemudian mengenali sifat yang digunakan dalam konstruksi mereka yang sesuai dengan hipotesis "nyata" yang mereka duga dan karenanya jaminan sifat ditemukan. Selanjutnya siswa diminta diminta untuk meninjau proses konstruksi, menjelaskan prosedur mereka, kami membantu mereka menangkap semua kondisi dalam masalah terbuka, menyadari apakah mereka memiliki dikenakan sifat tambahan atau pembatasan, dan memahami ketergantungan hubungan terlibat dan, oleh karena itu, logika di balik pernyataan dari bentuk jika ... kemudian ...

Seperti contoh: terdapat pernyataan "Dalam sebuah segiempat, jika diagonalnya membagi diagonal lainnya, maka segiempat merupakan jajar genjang ".

Siswa disuruh membuat dua buah garis yang tegak lurus dengan tombol line => Perpendicular bisector => buat lingkaran dengan pusat pada perpotongan garis tersebut dan jari2 pada masing-masing garis deng tombol Circle => tentukan titik  potong masing-masing lingkaran dengan masing-masing garis dengan tombol intersection point => buat segmen dari titik potong tersebut dengan tombol Segment => Hitung jarak dari titik potong garis yang tegak lurus dengan masing-masing titik potong lingkaran dengan masing-masing garis dengan tombol Distence and Lengt

Bangun geometri yang terbentuk adalah sebuah jajaran genjang sehingga dapat disimpulkan “Dalam sebuah segiempat, jika diagonalnya membagi diagonal lainnya, maka segiempat merupakan jajar genjang”

 Daftar Pustaka

Laborde, C.: 2000, 'Dynamic geometry environments as a source of rich learning contexts for the complex activity of proving ', Educational Studies in Mathematics 44, 151 - 161.

Mariotti, M.A.: 2000, 'Introduction to proof: the mediation of a dynamic software environment ', Educational Studies in Mathematics 44, 25 - 53.

Mariotti, M.A.: 2006, ‘Proof and Proving in Mathematics Education’, in A. Gutiérrez and P. Boero (eds.), Handbook of research on the psychology of mathematics education, Sense Publishers, Rotterdam, The Netherlands, pp. 173-204.

Radford, L.: 1994, 'La enseñanza de la demostración: Aspectos teóricos y prácticos', Educación Matemática, 6, 3, 21-51.

Temukan tulisan terkait:

"Belajar Geometri Dengan Cabri Geometri"