Bukti Geometri #16

Bukti Geometri #16

Oleh: Samsul Maarif

Masalah yang akan dibuktikan:

Jika terdapat sebuah segitiga ABC dengan titik P, Q dan R masing-masing pada sisi AB, BC dan AC dimana AQ, BR dan CP berpotongan di satu titik, maka berlaku: (AP/PB)×(BQ/QC) ×(CR/RA) = 1. (Teorema Ceva)

                          

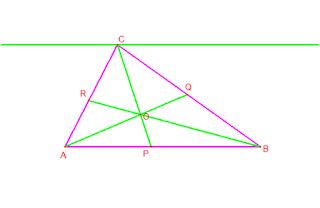
Sketsa permasalahan:

Bukti

Perhatikan bahwa titik C noncoliner terhadap AB sehingga menurut teorema Playfair dapat ditarik secara tungga garis //AB melalui titik C, seperti tampak pada gambar berikut.

 Selanjutnya berdasarkan Axioma 2 Euclid maka segmen AQ dan BR dapat diperpanjang hingga memotong garis //AB melalui titik C masing-masing di titik S dan T seperti tampak pada gambar berikut.

Perhatikan segitiga CRT dan segitiga ARB dimana besar sudut TRC = sudut ARB (bertolak belakang), besar sudut TCR = sudut RAB (sudut dalam berseberangan) dan besar sudut CTR = sudut ABR (sudut dalam berseberangan), berdasarkan prinsip kesebangunan dua buah segitiga maka segitiga CTR sebangun dengan segitiga ARB yang berakibat CR/RA = TC/AB…..(i). Perhatikan pula segitiga CQS dan segitiga ABQ dimana besar sudut CQS = sudut AQB (bertolak belakang), besar sudut QCS = sudut ABQ (sudut dalam berseberangan) dan besar sudut CSQ = sudut BAQ (sudut dalam berseberangan), berdasarkan prinsip kesebangunan dua buah segitiga maka segitiga CQS sebangun dengan segitiga ABQ yang berakibat CQ/BQ = CS/AB  <=> BQ/CQ = AB/CS……(ii).

Selanjutnya perhatikan segitiga AOP dan segitiga COS dimana besar sudut AOP = sudut COS (bertolak belakang), besar sudut APO = sudut OCS (sudut dalam berseberangan) dan besar sudut PAO = sudut CSO (sudut dalam berseberangan), maka segitiga AOP sebangun dengan segitiga COS yang akan berakibat AP/CS = OP/CO…..(iii). Berikutnya perhatikan juga segitiga segitiga BOP dan segitiga COT dimana besar sudut BOP = sudut COT (bertolak belakang), besar sudut BPO = sudut OCT (sudut dalam berseberangan) dan besar sudut PBO = sudut CTO (sudut dalam berseberangan), maka segitiga BOP sebangun dengan segitiga COT yang akan berakibat PB/CT = OP/CO…..(iv).

Berdasarkan pernyataan (iii) dan (iv) dapat dinyatakan bahwa AP/PB = CS/CT…..(v). Sehingga dengan mempertimbangkan pernyatan  (i), (ii) dan (v) dapat disimpulkan bahwa  (AP/PB)×(BQ/QC) ×(CR/RA) = 1. □

Daftar Pustaka

Fogiel. 1987.  The Geometry Problem Solver Plane, Solid and Analytic. New York: Research and Education Association 505 Eight Avenau.

Maarif, S. 2015. Pembelajaran Geometri Berbantu Cabri 2 Plus. Jakarta: In Media.