Bukti Geometri #29

Bukti Geometri #29

Oleh: Samsul Maarif

Masalah yang akan dibuktikan:

Buktikan bahwa tiap-tiap garis tinggi pada segitiga lebih pendek daripada setengah jumlah sisi yang mengapitnya.            

Sketsa permasalahan:

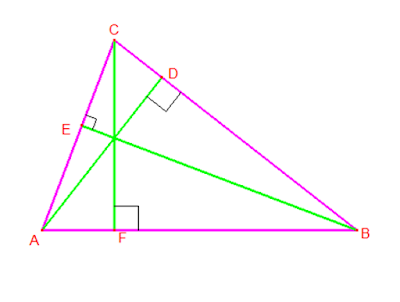
Diketahui AD, BE dan CF adalah garis tinggi segitiga ABC, akan ditunjukka bahwa (i) AD < ½ (AB+AC) dan (ii) BE < ½ (AB+BC) dan (iii) CF < ½(AC+BC).

Bukti

(i) Akan ditunjukkan bahwa AD < ½ (AB+AC)

Perhatikan segitiga ADC yaiti segitiga siku-siku di titik D, berdasarkan teorema 2 pertidaksamaan segitiga  karena besar sudut ACD < sudut ADC maka panjang AD < AC …..(a). Selanjutnya perhatikan segitiga ADB yaitu segitiga siku-siku di titik D, berdasarkan teorema 2 pertidaksamaan segitiga  karena besar sudut ABD < sudut ADB maka panjang AD < AB ….(b). Dari pernyataan (a) dan (b) dengan menjumlahkan kedua pertidaksamaan maka didapat AD < ½ (AB+AC).

.

Tanpa mengurangi keumuman dengan analogi cara pembuktian pada (i) maka dapat ditunjukkan (ii) BE < ½ (AB+BC) dan (iii) CF < ½(AC+BC).

Berdasarkan pernyataan (i), (ii) dan (iii) maka terbukti bahwa tiap-tiap garis tinggi pada segitiga lebih pendek daripada setengah jumlah sisi yang mengapitnya. □

Daftar Pustaka

Baan, MA. De & Bos, J.C,. 1992.  Ilmu Ukur untuk Sekolah Lanjutan tingkat Pertama. Jakarta: Pradnya Paramita.